圏論書籍紹介
圏論の書籍を紹介するゾ!
- Steve Awodey (2010) "Category Theory" Oxford University Press
- Saunders Mac Lane (1998) "Categories for the Working Mathematician" Springer
- Tom Leinster (2014) "Basic Category Theory" Cambridge University Press
- Masaki Kashiwara, Pierre Schapira (2005) "Categories and Sheaves" Springer
- Saunders MacLane, Ieke Moerdijk (1994) "Sheaves in Geometry and Logic" Springer
全部洋書になってしまったけど、僕は圏論のいい和書を知らないので…一応全部持ってる本で紹介してます。
順番に紹介すると
1〜3は圏論の基本的なことがだいたい学べるようになっています。
1は私が一番最初に圏論に触れた本で、絵がいっぱい書いてあり、例もそこそこ載っているので、おすすめですね。
和訳もありますが、クソ和訳なのでおすすめしません。洋書で書いましょう。
2は言わずもがなな圏論の基礎。和訳が圏論の基礎というタイトルですが、1〜3の中では一番とっかかりづらいと思います。
どうしても日本語の圏論の本が欲しいならこの和訳を持っとくといいかもしれません。
3はさっきつい電子書籍で買いました。パラパラとしか読んでないですが、絵を見てだいたい何を言っているかわかったので、良い本だと思います(雑)。
まあ良い本だという噂しか聞かないですし、実際例も丁寧に書いてありそうな雰囲気がしたので、今から圏論始めるにはおすすめかもしれません。
4と5についてはレベルが1段階上がります。
4は圏論の応用を考えるとこうなるって感じの本ですね。内容は割とホモロジー代数的な話もいっぱい書いてあるっぽいんですが、正直なところ層周辺の勉強の為に買ってその辺しか読んでないので、代数的な部分は読み飛ばしてしまってます。じゃあ紹介すんなって感じですが、まあそれだけでも十分価値がある本なので、全部読んで理解できる人は私に教えてください。
5も応用ちっくな内容になっていて、正直ここに書いてあることを理解することが大学院中の目標の1つでもあったりしましたが、まだいまいち理解できてないです。少なくとも幾何学と論理学の知識が前提知識として必要だと思います。
サーモンランで愉快な人たちと当たったw
どうも、ねりあです!
今回のサーモンランは全員クマさん印装備ということで、
最近サーモンランやってなかったんですが久しぶりにやってみました。
今初期値100だからこれを機に200にしとこうと思って挑みました!
が、なかなか勝てず…
なかなか勝てない要因としては
- 武器の癖が強い
- ノルマが高い
1については、武器の癖が強く、キルは取れるもののインク管理が大変、
気づいたら退路がなくなっているという状況が多かった気がします。
2については、普通にノルマ多くないっすかって感じですね。
しかもその割にみんなキルに集中して金いくら集めてくれない…
これは必ずしも僕のせいではないと思う…
こんな感じで、金イクラはそこそこ集まるものの、ゲージは上昇せずみたいなことを繰り返していました。
そして、200までは遠いけどもう1200集まるし次最後にしようとしたところで、愉快な人たちと当たりました。
しかもそういうのに限ってしっかり成功するっていう。
動画は撮ったんですが、わざわざ編集するようなものでもないかなと思うので、そのまま上げます。
あと、最近自分でギアを組んでみたので、今度その紹介をできたらなと思います。
なんとなくブログ書こうって思ったけど書く内容なかった
本当になんとなく、ブログを書きたい気分だった。
でも、よくよく考えると言いたいこと全部Twitterで言ってるんだよなぁ〜
で、思ったこととしては、ブログ書くのって難しいっすね。
僕個人的な理想のブログとしては、二種類で
- 本当にただ思っていることを言うだけのブログ
- ただただ学問的に正しいことが述べられたブログ
のどっちかを目指してて、逆に
- 論理的に確定できる事項でないことに対する評論ブログ
系はあんまり好きじゃないんだよなぁ〜
いや、ブログってそう言うもんでしょって言う人いっぱいいそうだし、何なら世の中そういうブログで溢れている気がするんだけども。
というか世の中の本でも評論文で少しでも意見の偏りが見えると嫌になってしまいますね。
ちゃんと賛否両方の意見を平等に扱った上で、あくまで筆者の意見としてであることがはっきりしている文章はむしろめっちゃ好き。
あ、このブログはただ僕が好きじゃないってだけで、ブログの評論とかじゃないんで!
↑こんな感じで気をつけないとすぐ評論チックになってしまうの、めっちゃ難しいなって思いました。
あと、このブログは「あえてわかりづらい文章にすることで評論チックにならないようにする」っていう僕が編み出したテクニックを用いていますね(ただちゃんとした文章を考えるのがめんどk)。
そんなこんなでブログ書くハードルを自分で勝手に上げまくってるせいで、なかなかブログを書けずにいるマンになってる。
ポケ森から学ぶ経済学の初歩
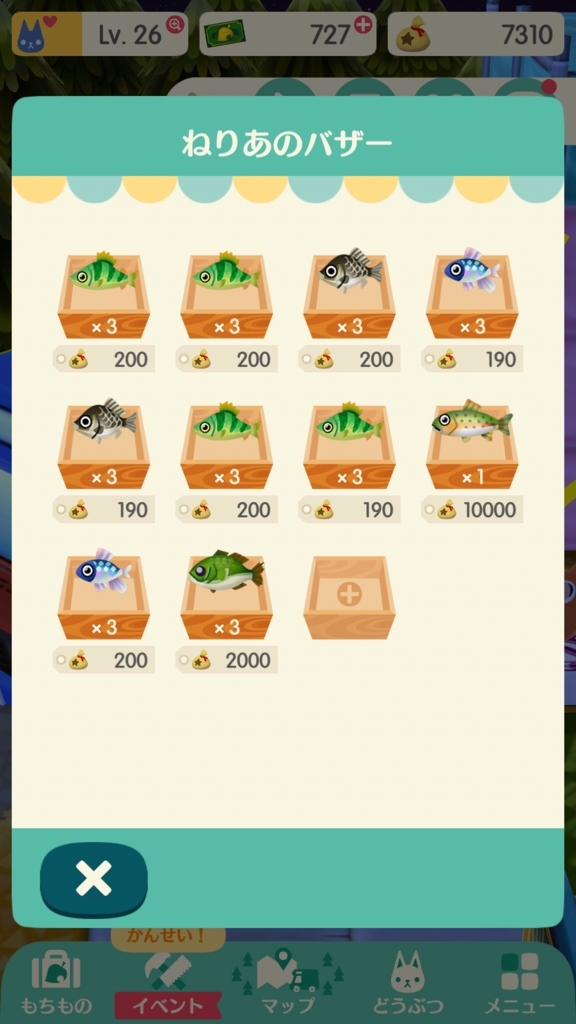
今流行のスマホアプリ、「どうぶつの森 ポケットキャンプ」(略してポケ森)について書こうと思います。
ポケ森についてと言っても、ポケ森でこの動物が〜とかこんなレア魚釣ったぜ〜とかそういう話ではなく、今回はバザー機能にのみ注目しました。
個人的にバザーという機能はとても面白いなと感じています。
その理由はちょっとした経済の勉強になるからです。
僕が小学生の頃読んだ本で「レモンをお金に変える法(ルイズ・アームストロング著)」という本があります。

この本はレモンからレモネードを作って売るというただそれだけの内容なのですが、どのように売れば儲けることができるのかという観点から経済学の初歩的考え方を一通り学べるようになっています。
今回のポケ森でもバザー機能で儲けるためにはどうすればいいか、一緒に考えてみましょう。
単価は?個数は?
最初にバザーに出店しようとして、まず悩むのはここでしょう。
もはやこれが決まれば今回の記事は終了なのですが、ここから考えないと話が進まないのでとりあえず考えて見ます。
まず、単価について考えてみましょう。
ポケ森では単価として設定できる上限額が決められています。
この額を今後「相場」と呼ぶことにしましょう。
相場はいまのところ3種類しかなく、100ベル、1000ベル、15000ベルの3つです(他にあればリサーチ不足です、ごめんなさい)。
そして、ポケ森ではこの相場の10分の1の価格でいつでも売却することができます。これより安い価格で売る意味はありません。
また、相場通りに売っても相場は設定できる価格の上限なので、相場より安い価格で売ってる人がいれば当然安い方を買うでしょう。
つまり、設定すべき単価をX、相場をSとして
という不等式が成り立ちます。
しかし、この間のどのくらいの価格に設定すれば買ってくれるのかはよくわかりません。
これは他のさまざまな情報を考慮しないと決まらないので後回しにしましょう。
次に個数についてです。
ポケ森ではまとめ売りができるようになっており、このまとめ売りの個数も重要なファクターとなっています。
個数も単価同様に最大値が決まっており、10個が最大となっています。
一つ例を挙げて考えて見ましょう。
相場1000ベルのものを半額の単価500ベルで10個まとめ売りをしたとします。
買う側は5000ベル払って10個買うわけですが、相場1000ベルのものというのは2日1回どうぶつ達から要求されるかどうかというものになっています。
つまり、いくら単価が安くても一気に10個もいらないわけです(ポケ森には持ち物の上限もあるので、邪魔になりかねません)。
もちろん買う側は1個ずつをたくさん売ってくれる方がありがたいですが、売る側はバザーに出品できる上限があるのでできる限りまとめて売りたいでしょう。
この問題を解決するためには、買う側がまとめて欲しい最小単位を知ることが出来れば良さそうです。
バザーで売買される品は基本的にどうぶつ達が要求している品です。
つまりどうぶつ達の需要がそのまま買い手の需要に繋がります。
相場毎に考えると、相場100ベルは一度に1~3個要求され、頻度も高いです。
相場1000ベルは時々1匹単位で要求されることがあります。
相場15000ベルは僕は今まで要求されたことがありません。今の所どうぶつ友好度20で要求されるという情報がありますが、真偽はわかりかねます。
以上のことを踏まえると
- 相場100ベル→3匹セット
- 相場1000ベル→1~3匹セット
- 相場15000ベル→1匹単品売り
ぐらいが良さそうです。
個数については結論が出ました。
結局単価は?
正直なところ周りとの価格競争次第なのですが、相場の半額以下は割に合わない気がします。
僕は最初9割で売っていたのですが相場100ベルはぼちぼち買ってくれる人がいるという感じだったので、そこまで格安にしなくても買ってくれる人は買ってくれます。
しかし、相場1000ベルは売れ残ったので900ベルではなかなか出してもらえないみたいです。
それを考慮すると6~8割程度が妥当でしょうか。
僕は相場100ベルと1000ベルを3匹ずつまとめ売りすることで、3の倍数にして単価を相場の3分の2の値段で売るというのを実践中です。
2匹買えば1匹タダって感じでわかりやすいですし。
その他小技
売るという観点で見て、実は単価や個数より重要なものがあります。
それは宣伝です。
でもポケ森で宣伝ってどうやればいいの?って感じですよね。
実際に宣伝そのものはTwitterやSNSで行うしかありません。
しかし、ただ「今自分のバザーでこんな感じで売ってます!」って常に発信することは困難です。
そこで、宣伝しやすい売り方を考えることが重要になってきます。
宣伝しやすい売り方とは?
要するに買い手にとってのわかりやすさです。
先ほどの単価の部分で説明した価格設定を全て相場の3分の2に統一するというのも一つのテクニックです。
ということで僕は川魚を相場の3分の2の価格で売ってます!!!
川魚を買うならぜひ「ねりあのバザー」で!!!
フレコ:5975 4903 806
フレンド登録も受付中!!!
という感じで露骨に宣伝するといいと思います。
もう一つ小技としては僕は途中で気づいて実践し始めたんですが、10,20ベルぐらい下の価格設定にすることですね。
人には10000ベルと9980ベルで20ベルしか変わらなくても9980ベルの方がかなり安く見えるという錯覚があります。
ぜひ実践してみるといいと思います。
まとめ
こんな風に、ポケ森のバザーは経済が学べる面白い要素だと思います。
ぜひ一度考察してみてはどうでしょうか。
そして、冒頭で紹介したレモンをお金にかえる法ではこれ以上にもっと原価やレモンの賞味期限等多くの経済学的要素を含み話が展開していきます。
興味を持った方はぜひ一読してみてはいかがでしょう。
それでは今回はこれで!
どう頑張っても自分のデッキに勝てません
僕は2つデッキを持っています。
1つは昨日の大会で見事優勝したグソクゾロアです。
こっちは大会で使うデッキとして用意しています。


そしてもう一つがアローラキュウコンデッキです。

暇な時はよく1人で回したり、知人に手伝ってもらって自分のデッキ同士で対戦させたりしているのですが、今の所アローラキュウコンの全勝です。
じゃあアローラキュウコンの方が強いのでは?ってなるんですが、そういうわけでもないんですよねぇ…
アローラキュウコンGXというカードは本当にダメージレースでは強いカードだと思います。
なので、グソクムシャや今流行りのルガルガンにはなかなか負けないと思います。
しかし、一撃で高火力を出すサーナイトデッキや鋼タイプを主軸としたデッキにはまず勝てません。
そしてスピード感はないので、速攻性の高いマッシブーンにも勝てるか怪しいと考えています。
というわけで11月26日のチャンピオンズリーグにどっちで出ようかとても悩んでいます。
グソクゾロア→戦えるデッキの幅が広いが、常に安定して勝てるとは言えない
アローラキュウコンGX→ダメージレースでは安定して勝てるが、高火力デッキに苦戦を強いられる可能性と事故率はこっちの方が高い
うーん、ちょっとまとめてみた感じだと、アローラキュウコンGXの事故率を減らして環境の様子を見ながら調整した方がいいかもしれないですね。
次のジムバトルではアローラキュウコンで出ようかなぁ
ポケモンカードジムバトルに参加してきました。
今日はポケモンカードジムバトルに参加してきました。
場所は池袋のホビーステーション。
あいにくの大雨で「これは参加者少ないかもなぁ…」と思いながら、知人のしーさんと一緒に参加。
始まってみると参加者は10人でした。
皆さん大雨の中よく来るよなぁって人のこと言えませんがw
僕はゾロアークGX&グソクムシャGXのデッキでの参加です。


1試合目
ということで1試合目スタートです。
相手は小学生になるかならないかぐらいの男の子、どうやら父親と揃っての参加のようです。
だいたい親子で参加しているパターンは英才教育を受けているので、全く油断できません。
じゃんけんで勝ち、先行を取り最初のポケモンをめくると、自分はコソクムシ、対して相手はウソッキー。
うーん、ウソッキーだけじゃまだ何のデッキかわからない上にこっちは展開しづらくなってしまいました。
ひとまず手札にあったあずさを使い、ゾロア、コソクムシ、カプ・コケコの3体で埋めてしまいました。
ウソッキーを倒さない限りもうこれ以上出せません。
次の相手のターン。
なんやかんやして手札から出てきたのはイワンコ。
これ今超絶流行ってるルガルガンデッキってやつやん…w


本当に子供だからと言って油断できませんが、あいにくこっちはグソクムシャ、相性が悪いかなぁ…
というわけで大人げなく勝ってしまいました。
相手のデッキ、ルガルガン以外はレジロックEXやストロングエネルギー等火力アップ系ギミックが多く、スピード促進系カードが少なかったので、そこはまだ子供らしいというかなんと言うか。
とりあえずゾロアークGXと組んでるみたいな英才教育を受けてなくてよかったw
2試合目
相手はラランテスGXデッキ。

僕のデッキも含め、こう言った1進化ポケモンでスピードとほどほどの火力と耐久のバランスを兼ね備えたデッキ構築はカードゲーム業界で所謂ビートダウンに当たるんですが、ポケモンカードではビートダウンって言葉はあまり使いません。
なぜならビートダウンって技名を持ったポケモンがいるから。
〇〇ビートダウンって言うとなんか〇〇とビートダウンって技を持ったポケモンを組み合わせたデッキみたいに見えてしまう。
しかもそのビートダウンって技を持ったポケモンがややこしいことに古いゾロアークで、今流行ってるゾロアークGXとごっちゃになりやすいんだよなぁ。
相手はラランテスGXを主軸としてゾロアークGXでスピード促進していくデッキ。
ラランテスGX自体はとてもバランスの取れているカードなんですが、グソクムシャGXと戦うにはちょっとスピードが足りなさそう。
危なげなく勝つことができました。
3試合目
基本的に勝ち点の高いもの同士が当たるので、相手もすでに2勝してます。
相手のデッキはゾロアークドータクンデッキ。
そうきたかって感じですね。


特殊エネルギーに頼らず鋼エネルギーを回していくスタンス。
速さも火力も申し分ないのでなかなか強敵。
グソクムシャGX VS ゾロアークGX
僕「じゃあ、であいがしらでゾロアークに120ダメージです。」
相手「アセロラで回収、後ろのゾロア進化させてライオットビートでグソクムシャに120です。」
僕「アセロラで…後ろのグソクムシャでであいがしら。」
相手「バトルサーチャーからのアセロラ、ライオットビート。」
僕「バトルサーチャーでアセロラ…であいがしらで…」
とても不毛。
そのあととても接戦をした後、勝利することができました!
最終結果
ということで全3戦で結果発表!
もちろん3戦全勝したので優勝です!
やったー!
考察
環境的にはゾロアークGXを使ったダメージレースを持ちかけるデッキが多いイメージです。
メインに添えるポケモンはスピードと火力にバランスが取れている1進化GXポケモンを採用するのが主流ですね。
もっとも流行っているルガルガンはゾロアークに対して弱点を取れるというのが強みです。
そこに弱点を取れるグソクムシャは現環境に刺さっていると言ってもいいと思います。
また、今回ピン刺しで採用したカミツルギGXですが、やはり環境的に特殊エネルギーに頼ったデッキが多く(人のこと言えない)とても有効なカードだったと思います。

また、その他デッキの種類としてはダメージレースでスピード特化のマッシブーンGX、高火力一撃ダウンを狙うサーナイトやソルガレオ、ラフレシアやダストダスのロック、ジュナイパー等のダメージギミック系が挙げられますが、環境的に何よりもスピードが求められている気がするので、高火力系とロック系は相当速いまたは遅延能力が高くないと難しいと感じました。
AIの勉強会に参加した話、本当のタイトルは最後の1文に
どうも、最近あんまり余裕がないねりあです。
「余裕がない」というのも、仕事をしているとどうしても時間的余裕はなくなってしまうんですよね。
時間的余裕がなくなると精神的余裕も無くなりがちで、視野が狭くなったり、物事を楽しめなくなってしまったりするんですが、こういうのは良くないですよね。
ところで今日は機械学習の勉強会に参加してきました。
機械学習の勉強会と言っても、数学メインで機械学習に関係のある話をしようというもので、これなら参加しやすいかなと思って参加した感じです。
そもそもAIには興味があるものの体系的なものを何も知らなかったので、そういうのも少し知れて良かったですし、何より議論みたいなことが出来て楽しかったです。
機械学習の勉強のモチベも格段に上がりました。
人生可能な限り楽しいことをやるっていうのが僕のモットーですし、時間的余裕がないときこそ精神的余裕をもって、急がば回れの精神でやっていきたいなと思うので、今からスプラトゥーンをやります。
以上、スプラトゥーンを一緒にやってくれるフレンドを募集する話でした。